Risco e covariância - Como otimizar a alocação de ações num portfólio? Parte 1

Fala pessoal! Tudo bem?

Estive afastado aqui do blog por alguns meses devido à falta de tempo por algumas mudanças na minha vida. Saí do Itaú e entrei no grupo XP em agosto, e precisei de um tempo para me reorganizar. Com tudo em ordem novamente, chegou a hora de retomar os estudos do mercado financeiro! 

Resolvi criar uma série de posts abordando um tópico que é importantíssimo na vida do investidor de longo prazo: a alocação ótima de ativos num portfólio. Nós já estudamos quais são as melhores formas de se encontrar os papéis para compor um portfólio, mas não abordamos a melhor maneira para alocar essas ações depois que elas foram escolhidas, isto é, quais ações devem ter maiores pesos, de forma a obter os melhores resultados? Como otimizar a alocação do portfólio por alguma métrica, como maximizar o retorno e reduzir o risco?

Há muitas formas de promover essa alocação, mas nessa série vamos usar o procedimento chamado de “Otimização por Média-Variância”, que faz parte da Teoria Moderna do Portfólio, introduzida em 1952 por Harry Markowitz, teoria pela qual ele foi premiado com um prêmio Nobel em economia.

O nosso problema basicamente é o seguinte: Dado um conjunto de ações, e um retorno alvo que queremos obter, qual a alocação de cada ação de forma a minimizar o risco do portfólio? 

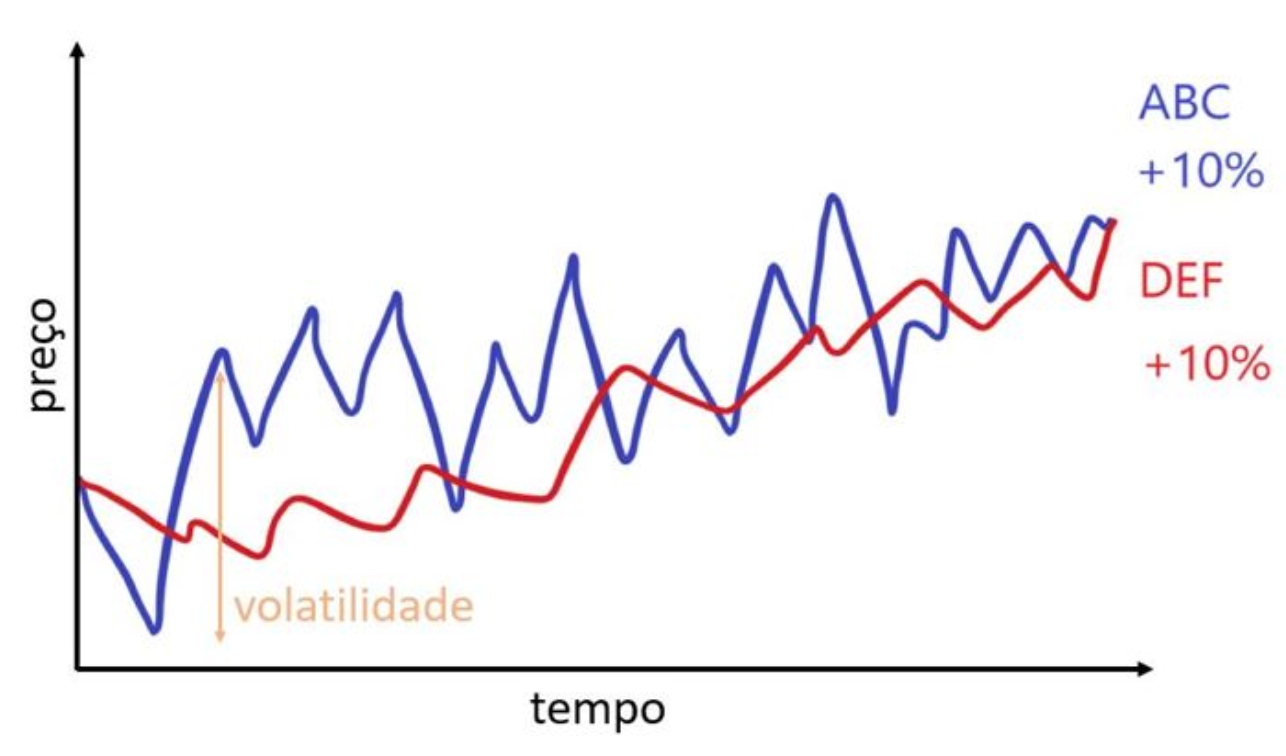
Primeiramente precisamos entender o que é o risco. O desvio-padrão dos retornos de um papel é um indicativo de sua volatilidade. É essa volatilidade que usamos como uma medida do risco. Para entender melhor, vamos comparar duas ações fictícias, mostradas no gráfico abaixo. O papel ABC subiu 10% ao longo do ano, mas foi muito volátil. O papel DEF também subiu 10%, mas de uma forma bem menos volátil. É essa volatilidade, como mostrado pela seta laranja no gráfico, que nós usamos como uma medida do risco, e é simplesmente o desvio-padrão dos retornos diários.

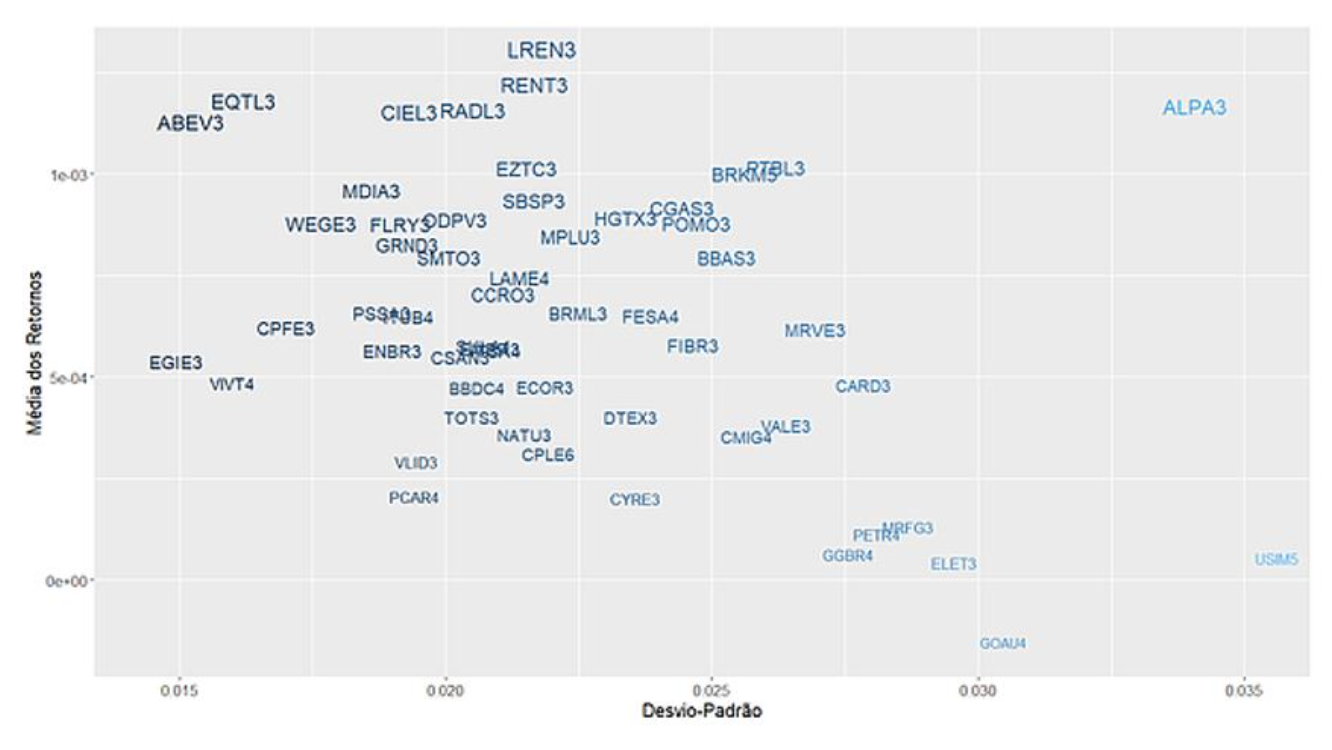
Ao criar um portfólio, é interessante considerar o retorno vs. o risco de vários papéis para diminuir o risco total. Uma maneira de se fazer isso é plotando o retorno e desvio-padrão de vários papéis, como fizemos nesse post aqui:

 

Se criássemos um portfólio com ABEV3, ALPA3, EGIE3 e USIM5 em proporções iguais, ele estaria localizado mais ou menos no seguinte lugar do gráfico:

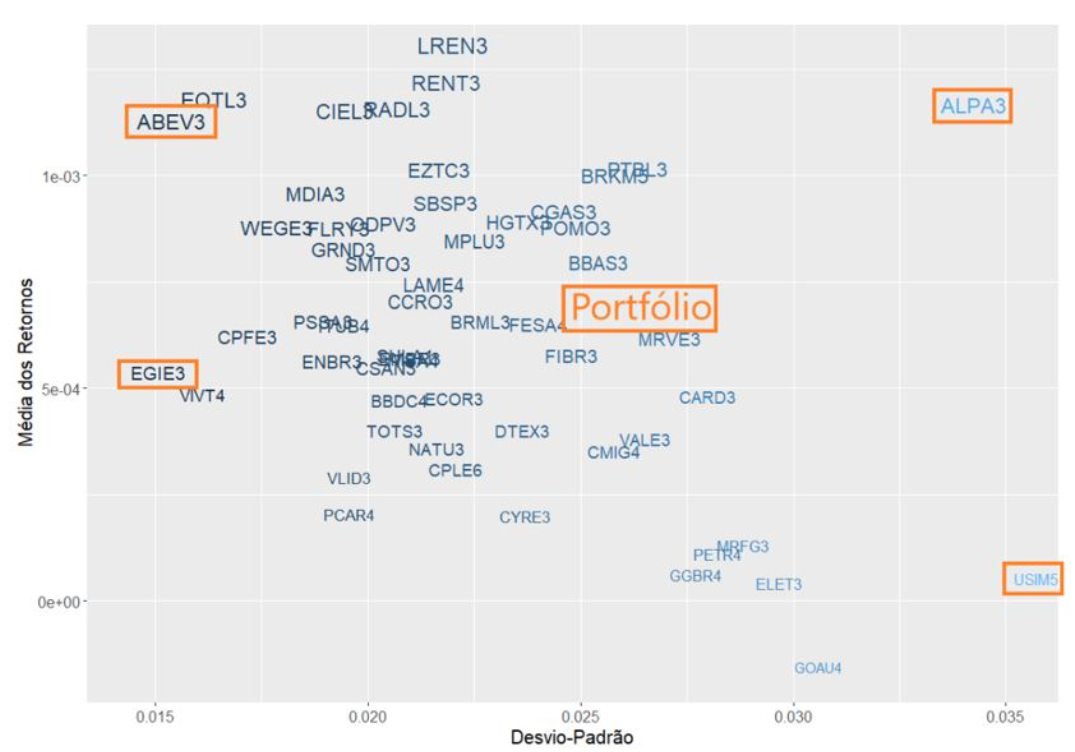
E se deslocaria no gráfico dependendo dos pesos que déssemos para cada uma das ações, ex.: aumentaria os retornos se colocássemos mais ALPA3, mas ao mesmo tempo teria um maior risco.

Será que conseguimos criar um portfólio que se localiza no canto superior esquerdo do gráfico, mesmo que nenhum dos papéis esteja naquela posição?

A resposta é sim, graças ao trabalho de Markowitz, que descobriu a relação entre ações em termos de suas covariâncias. Segundo sua teoria, o desempenho de um portfólio (especialmente em termos de risco) não é apenas um fator resultante dos vários riscos alocados, mas tem a ver com a forma como as ações interagem entre si diariamente. Assim, se escolhermos as ações certas nas proporções certas, podemos ter um portfólio que tem um risco menor que o risco de todas as ações que o compõem! 

A importância da covariância 

Suponha que temos três ações: ABC, DEF e GHI, que desempenharam ao longo do ano como mostrado no gráfico abaixo:

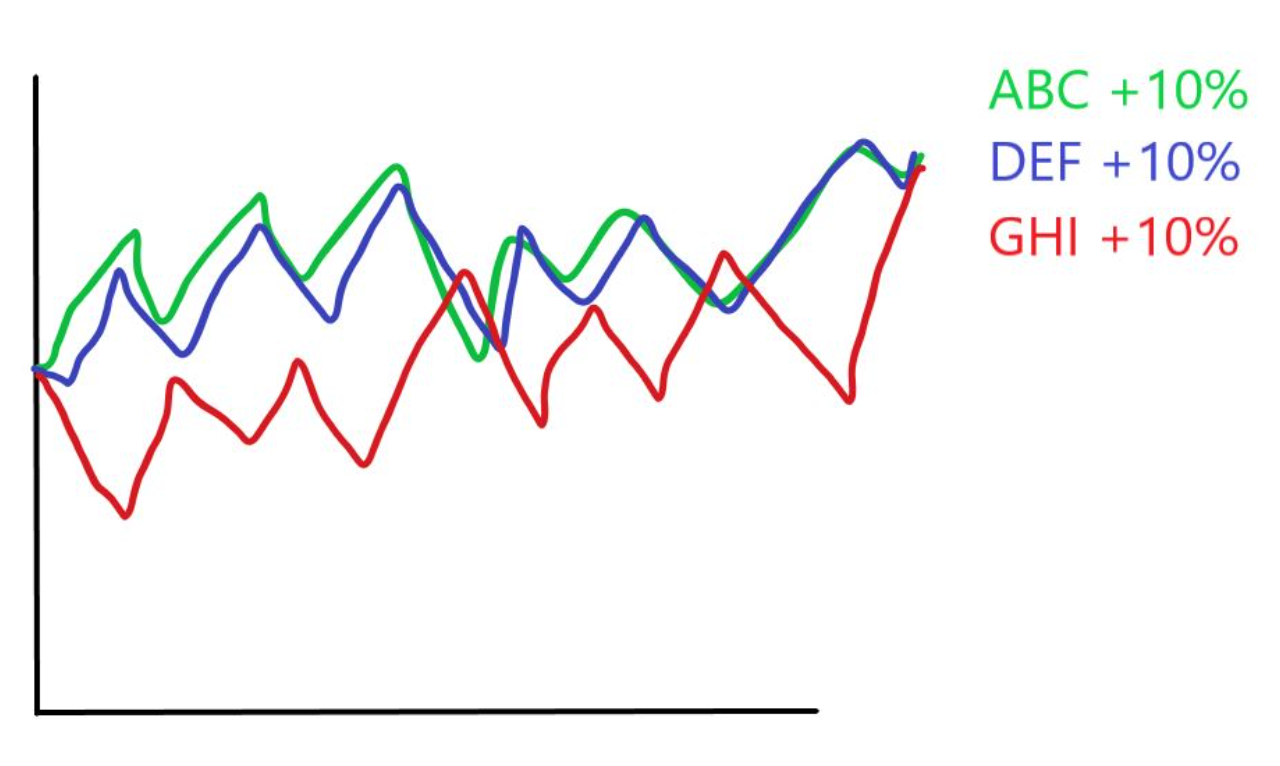
Vemos que todos os papéis subiram 10%, e que os papéis ABC e DEF tiveram curvas praticamente idênticas, enquanto que GHI teve um comportamento oposto aos dois anteriores (tende a subir enquanto ABC e DEF descem, e vice-versa) embora tenha tido o mesmo retorno. De forma sucinta, isso quer dizer que ABC e DEF têm uma covariância alta e positiva, mas GHI têm uma covariância alta e negativa com ABC e DEF.

Qual o melhor portfólio que podemos criar combinando essas três ações? Se utilizarmos as duas ações de covariância positiva com os pesos de 50% para cada, teríamos o seguinte portfólio:

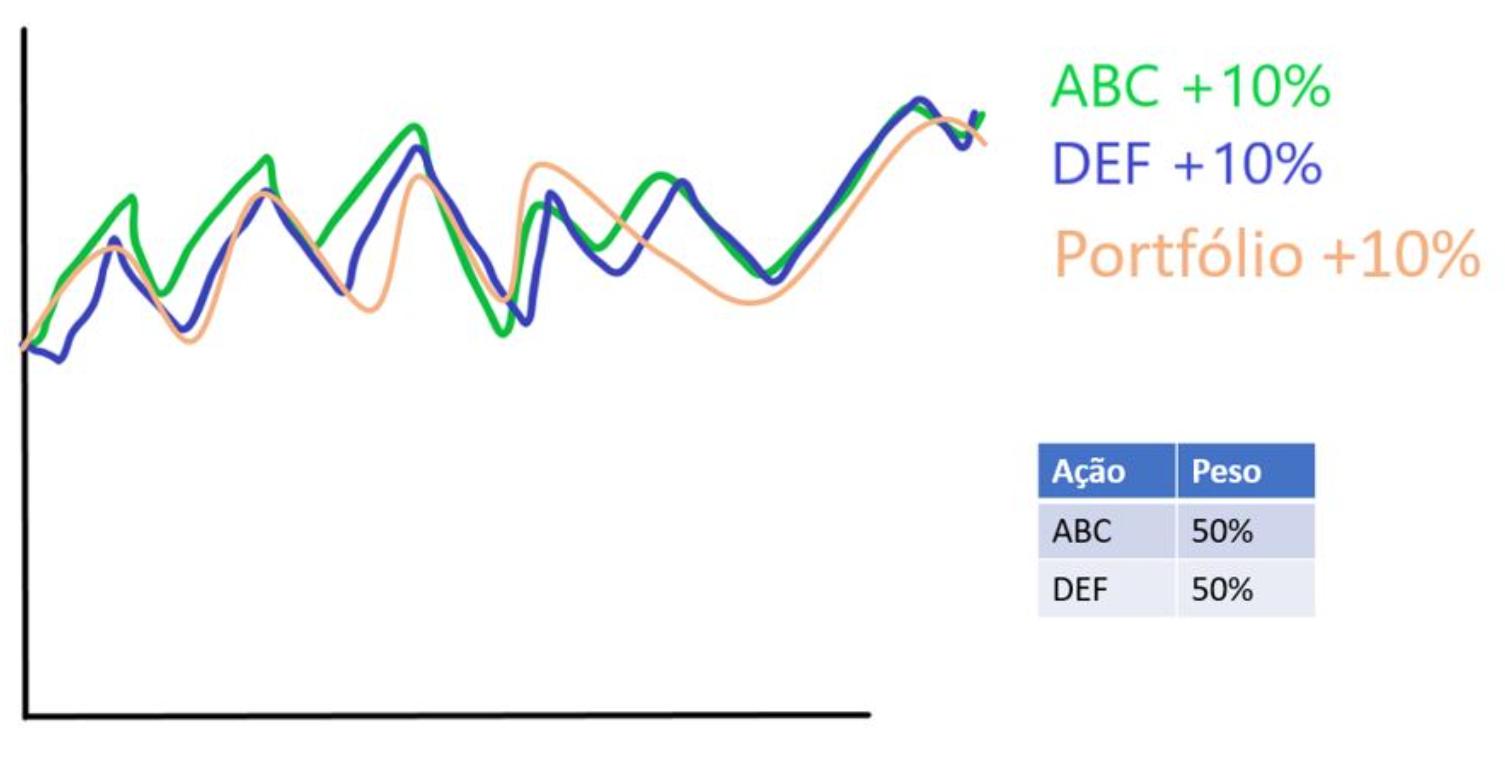
Que, como o gráfico mostra, não seria muito vantajoso pois teria um comportamento muito parecido com aqueles de ABC e DEF, renderia os mesmos 10% com um risco parecido com o das duas. E se além dessas duas ações, incluíssemos GHI, sendo o portfólio composto de 25% de ABC, 25% de DEF e 50% de GHI? O resultado seria o seguinte:

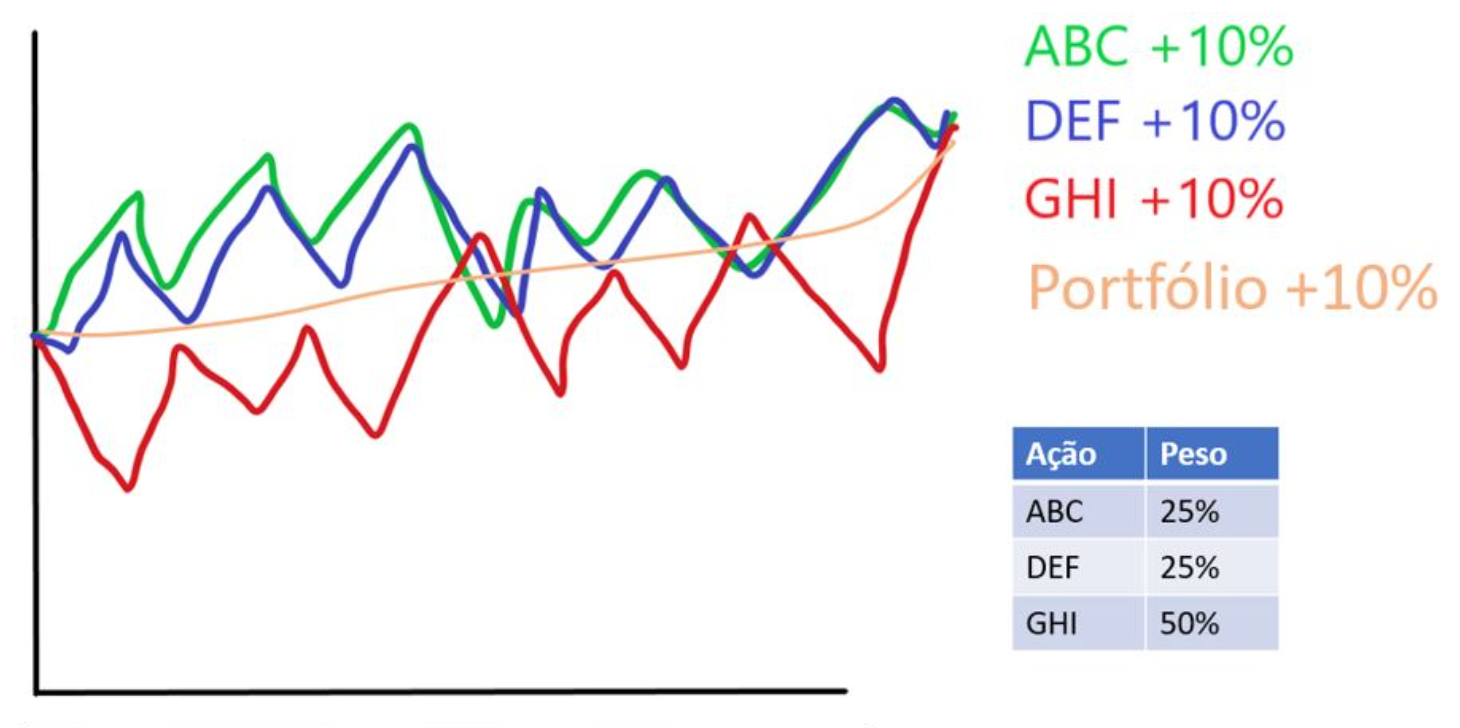
Ou seja, teríamos os mesmos 10% de retorno, mas com risco e volatilidade menores que qualquer uma das ações separadas! Possui uma curva muito mais suave, já que selecionamos papéis que são anticorrelacionados. Esse é um dos principais pontos da teoria de Markowitz: podemos alterar o retorno e risco de um portfólio através de diferentes combinações de ativos, uma vez que a interação entre eles é que vai determinar o desempenho final.  

No post seguinte vou apresentar a técnica de Otimização por Média-Variância e como ela leva todos esses conceitos em consideração na hora de calcular a alocação ótima para cada ação. Depois vou falar da “Fronteira Eficiente” e como determinar o menor risco possível para um portfólio dado um retorno alvo. Por fim, vou fazer uma simulação com os papéis escolhidos na série anterior para determinar a alocação ótima de cada um deles. Fiquem ligados!

#markowitz #mpt #mvo #portfolio #stocks #ações #risco #volatilidade #correlação #covariância