Fronteira Eficiente - Como otimizar a alocação de ações num portfólio? Parte 2

Fala pessoal!

Como vimos no post anterior, a grande contribuição que Markowitz trouxe ao mundo dos investimentos foram as suas considerações sobre o efeito da covariância entre as ações individuais e como ela impacta o risco do portfólio final.

Podemos ter um portfólio com um risco muito mais baixo se combinarmos ativos que são negativamente correlacionados porque quando um subir o outro cairá e vice-versa, e assim teremos uma volatilidade muito menor. O que procuramos no final é uma correlação negativa no curto prazo e correlação positiva no longo prazo.

Há uma série de algoritmos diferentes para se chegar ao portfólio ótimo para cada combinação de ações. O algoritmo que mais ganhou destaque desde então foi o Mean-Variance Optimization, ou Otimização por Média Variância, que vamos estudar agora.

Suponha que temos um conjunto de ativos e queremos descobrir como eles devem ser alocados analisando suas covariâncias, entre outras coisas. Vamos supor que para montar nosso portfólio de ações tivéssemos que escolher entre os seguintes papéis:

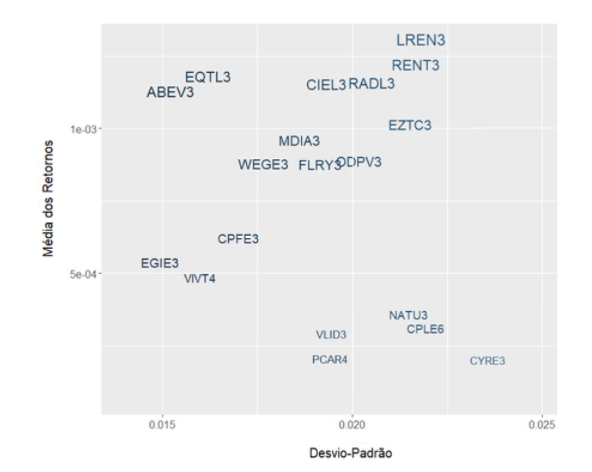
Dadas todas essas considerações, desse post e do post anterior, como podemos usar nosso otimizador (algoritmo de otimização, nesse caso o MVO), para encontrar a alocação ótima?

Para utilizar o algoritmo de otimização, devemos informar (como inputs) os seguintes dados:

• Retornos esperados: são os retornos que esperamos obter individualmente com cada papel, ao final do período que estamos considerando;
• Volatilidade: quão volátil tem sido cada papel em um dado período. Quanto maior o histórico, mais robustas serão as previsões;
• Covariância: medida da variabilidade (ou interdependência) entre dois papéis. É uma medida da correlação entre papéis, pois covariância zero indica falta de correlação;
• Retorno alvo: o retorno que queremos obter com o portfólio que vamos montar.

Como resultado, o modelo nos informará os pesos para cada um dos papéis que fornece o retorno alvo que estamos esperando e minimiza o risco, como mostra a figura abaixo:

E aí você pode estar se perguntando: como que teremos um risco final menor do que o risco de todas as ações no nosso portfólio?

Isso é possível justamente por levar em consideração as covariâncias entre as ações na hora de encontrar as alocações ótimas! Logo, se tivéssemos esse conjunto de ações, nós esperaríamos um portfólio com retorno equilibrado entre as ações e um risco menor que todas as ações juntas. Se estivéssemos considerando as ações individualmente, não seríamos capazes de encontrar as combinações corretas que nos traria ao ponto vermelho marcado no gráfico.

O conceito da fronteira eficiente 

Podemos perceber que para cada nível de retorno alvo, há um portfólio ótimo. Logo, vamos supor que temos diferentes níveis de retornos esperados, como mostrados no gráfico a seguir. O ponto em vermelho denota onde ficariam os portfólios com os riscos mínimos dados os retornos que queremos obter:

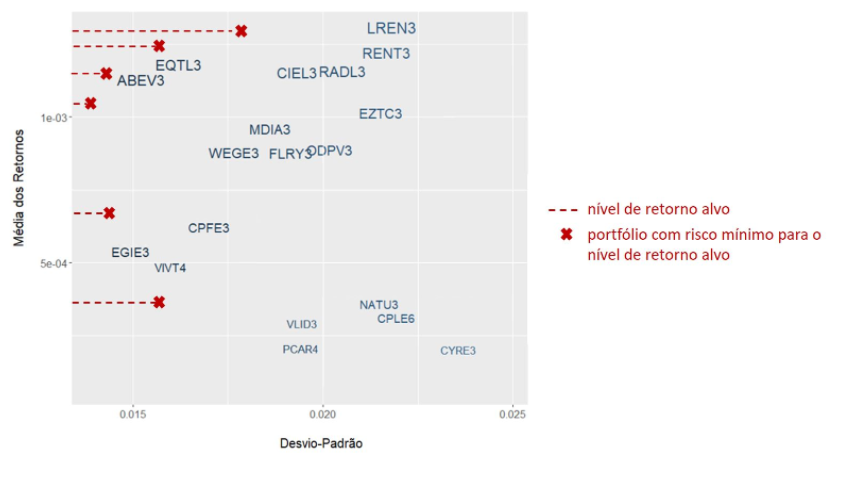
Em outras palavras, esses portfólios refletem os pesos de todas essas ações que nos dá o menor risco para cada retorno alvo. Agora, podemos fazer esse cálculo para todos os retornos possíveis, do mínimo até o máximo. Se fizermos isso, vamos obter uma curva, como mostrado a seguir:

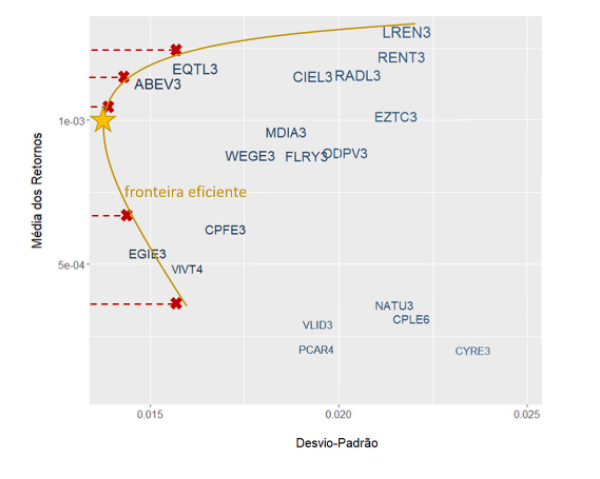
Essa curva é chamada de fronteira eficiente na teoria de Markowitz. Ela determina qual o risco que teremos dado um retorno alvo que queremos atingir. O portfólio de máximo retorno nesse caso seria obviamente aquele constituído apenas de LREN3, já que no nosso gráfico ela é a ação de maior retorno. À medida em que reduzimos o retorno alvo, nós encontramos vários outros portfólios com pesos diferentes para cada ação, até atingirmos aquele de menor risco, mostrado como uma estrela amarela.

Interessante notar que ao reduzirmos nosso retorno alvo, muitas vezes a fronteira eficiente faz uma curva na direção contrária, aumentando o risco. Por isso, na prática, a maioria das pessoas analisa a curva da estrela para cima, afinal quem quer um portfólio com menor retorno e maior risco, não é mesmo?

Como vocês já podem ter imaginado, não existem portfólios acima da fronteira eficiente, e todos os portfólios que se localizam abaixo dela são sub-ótimos de alguma forma.

Então, se tivéssemos um portfólio sub-ótimo, mostrado como o ponto vermelho na figura a seguir, ele teria o mesmo nível de retorno que o portfólio A, mas teria um risco bem maior, e teria o mesmo risco que o ponto B, mas com um retorno bem menor.

Assim, qualquer portfólio abaixo da fronteira eficiente não é eficiente porque tem um risco maior ou retorno menor que teria caso estivesse sobre a curva.

Com esse post então finalizamos todos os conceitos teóricos para entender o sentido das ideias de Markowitz sobre otimização de portfólios.

O próximo passo agora é partir para a prática. No próximo post vou mostrar em um exemplo prático com dados reais de alguns papéis da nossa bolsa como podemos usar o algoritmo de Otimização por Média-Variância para traçar a fronteira eficiente e encontrar a alocação ótima de menor risco. Até breve!

#covariância #risco #ações #portfolio #mvo #markowitz #fronteiraeficiente #efficientfrontier #correlação